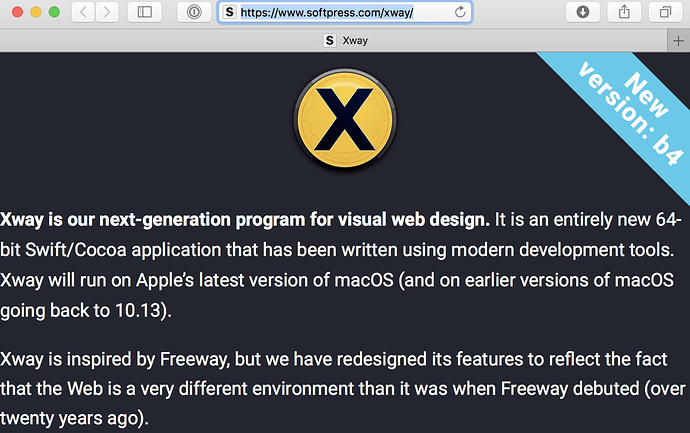
I must first admit my feature ignorance because I’ve not used XWAY very much. I am much more well versed in Freeway Pro 7 than XWAY. But I do see a distinct lack of left/right margins on the main Xway page here when shrinking the browser width.
Here’s a screenshot showing the browser width shrunk to the point where the white text slams right against the very edges of the browser window, with no margin at all.
You must admit this does look rather odd. One would expect at least a tiny bit of space between the leftmost and rightmost browser window edge and the start or end of the text block. I noticed this today after having read the post of another person in this forum who showed an example of his site, and when I browsed his site, he had the same problem with text slamming against the edge of the browser.
But the way, this isn’t just a desktop browser issue either. Here’s a screenshot of the iOS Simulator…
I suppose it doesn’t look too bad on an iPhone that is black because the LCD isn’t edge to edge on the entire front face of the iPhone. So it gives the illusion of a left/right margin. But in terms of the LCD alone, there is no left/right margin at all, as you can clearly see.
Perhaps even more problematic is the fact that some element on the same page ram right up against each other, as the word “Unlimited” smashes right against the word “Webfont” in the screenshot below…
Not sure if this is a feature limitation of XWAY or simply a design oversight, but I wanted to mention it nonetheless. My intent is not to criticize but merely to voice an observation I had today.
Thanks,
James